Pora na przedstawienie algorytmu ukrywania danych, który będzie odporny na kompresję JPEG. Zdecydowałem się na algorytm przedstawiony przez Jian Zhao i Eckhard Koch’a w 1996 roku. Jest on już trochę leciwy, ale posiada dobre wyniki odporności na kompresję.
Algorytm operuje w przestrzeni częstotliwościowej obrazu, więc nie zmieniamy poszczególnych pikseli. Do przejścia w przestrzeń częstotliwościową wykorzystywana jest transformata kosinusowa.
DCT
Dyskretna transformata kosinusowa (ang. discrete cosine transform) jest jedną z najpopularniejszych blokowych transformacji danych. DCT przekształca skończony ciąg N liczb f(0), f(1),…,f(N-1), w ciąg liczb rzeczywistych F(0), F(1),…,F(N-1) zgodnie z następującymi zależnościami:

Definiuję się również odwrotną transformatę kosinusową
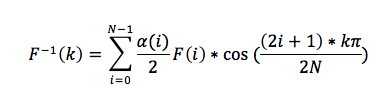
Podczas kompresji danych używana jest dwuwymiarowa transformata kosinusowa zadana wzorem:
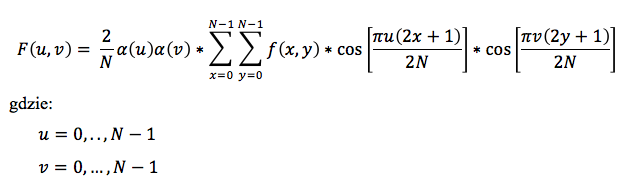
oraz przy dekompresja odwrotna:
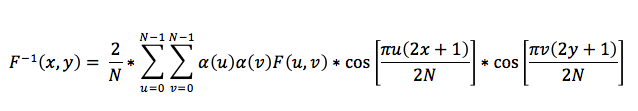
Algorytm Zhao & Koch
W algorytmie zaproponowanym przez Jian Zhao i Eckhard Koch’a również zostały zastosowane elementy algorytmu kompresji JPEG. Autorzy zauważyli, że skwantyzowane współczynniki DCT mają umiarkowany poziom wariancji w środkowym zakresie częstotliwości. Niewielkie zmiany w tych współczynnikach, nie powinny być zauważalne dla oka ludzkiego. Dlatego do wstawienia znaku wodnego należy wybrać trzy współczynniki ze środkowego zakresu. Po spełnieniu odpowiednich zależności pomiędzy tymi elementami będzie możliwość umieszczenia wiadomości w obrazie.
Relacje pomiędzy trzema współczynnikami tworzą 9 kombinacji (wzorów), które zostały podzielone na trzy grupy: dwie do zakodowania „1” lub „0” oraz jednej nieprawidłowej. Jeśli potrzebne są zbyt duże modyfikacje, aby zakodować bit (w taki sposób zmienić współczynniki, by pasowały do poprawnego wzoru) wtedy blok jest nieprawidłowy. W takim przypadku trzy współczynniki należy zmodyfikować do niepoprawnego wzoru, aby blok został pominięty przy odczytywaniu wiadomości. Kryterium wyboru prawidłowego bloku jest parametr MD(ang. maximum difference), czyli maksymalna różnica pomiędzy dwoma wybranymi elementami.

W powyższym obrazie znajdują się możliwe pozycje współczynników transformaty kosinusowej dla bloku 8×8. Zostały one statystycznie wybrane przez autorów algorytmu. Tak jak to zostało wspomniane wcześniej, do zakodowania wiadomości należy użyć trzech współczynników. Możliwe kombinacje tych trzech elementów znajdują się w tabeli poniżej.
| Nr wzoru | (k1,l1) | (k2,l2) | (k3,l3) |
| 1 | 2(0,2) | 9(1,1) | 10(1,2) |
| 2 | 9(1,1) | 2(0,2) | 10(1,2) |
| 3 | 3(0,3) | 10(1,2) | 11(1,3) |
| 4 | 10(1,2) | 3(0,3) | 11(1,3) |
| 5 | 9(1,1) | 2(0,2) | 10(1,2) |
| 6 | 2(0,2) | 9(1,1) | 10(1,2) |
| 7 | 9(1,1) | 16(2,0) | 2(0,2) |
| 8 | 16(2,0) | 9(1,1) | 2(0,2) |
| 9 | 2(0,2) | 9(1,1) | 16(2,0) |
| 10 | 9(1,1) | 2(0,2) | 16(2,0) |
| 11 | 10(1,2) | 17(2,1) | 3(0,3) |
| 12 | 17(2,1) | 10(1,2) | 3(0,3) |
| 13 | 10(1,2) | 3(0,3) | 17(2,1) |
| 14 | 3(0,3) | 10(1,2) | 17(2,1) |
| 15 | 9(1,1) | 16(2,0) | 17(2,1) |
| 16 | 16(2,0) | 9(1,1) | 17(2,1) |
| 17 | 10(1,2) | 17(2,1) | 18(2,2) |
| 18 | 17(2,1) | 10(1,2) | 18(2,2) |
Natomiast poniżej zostały przedstawione możliwe wzory trzech wybranych współczynników.
| (k1,l1) | (k2,l2) | (k3,l3) | |
| Wzór do zakodowanie „1” | H | M | L |
| M | H | L | |
| H | H | L | |
| Wzór do zakodowanie „0” | M | L | H |
| L | M | H | |
| L | L | H | |
| Nieprawidłowy wzór | H | L | M |
| L | H | M | |
| M | M | M |
Do dostosowania widoczności i odporności znaku, służą dwa parametry: MD oraz d. Parametr MD został omówiony wyżej. Natomiast parametr d definiowany jest, jako moc wstawienia wiadomości do obrazu. W rzeczywistości, jest to odległość pomiędzy dwoma wybranymi współczynnikami transformaty. Jego domyślna wartość to 1. Im wyższy parametr d, tym wstawiony znak będzie odporniejszy na modyfikacje, jednak należy się liczyć z większą widocznością i podatnością na ataki.
W poniższych algorytmach przyjąłem następujące oznaczenie:
Yq(k, l)– skwantyzowane współczynniki transformaty bloku
Sprawdzenie możliwości zapisu
wybierz pozycję współczynników (k1,l1),(k2,l2),(k3,l3)
Yq(k1,l1)=dct(k1,l1), Yq(k2,l2)=dct(k2,l2), Yq(k3,l3)=dct(k3,l3)
If bit=1
if MIN(|Yq(k1,l1)|,|Yq(k2,l2)|)+MD<|Yq(k3,l3)| then
zmodyfikuj blok do niepoprawnego wzoru
wstaw zmodyfikowane współczynniki do bloku
else
blok jest prawidłowy
end if
else
if MAX(|Yq(k1,l1)|,|Yq(k2,l2)|)>|Yq(k3,l3)|+MD then
zmodyfikuj blok do niepoprawnego wzoru
wstaw zmodyfikowane współczynniki do bloku
else
blok jest prawidłowy
end if
end if
Sprawdzanie możliwości odczytu
wybierz pozycję współczynników (k1,l1),(k2,l2),(k3,l3) Yq(k1,l1)=dct(k1,l1), Yq(k2,l2)=dct(k2,l2), Yq(k3,l3)=dct(k3,l3) Sprawdz czy Yq(k1,l1),Yq(k2,l2),Yq(k3,l3) są poprawnym wzorem
Wstawianie znaku
wybierz pozycję współczynników (k1,l1),(k2,l2),(k3,l3) Yq(k1,l1)=dct(k1,l1), Yq(k2,l2)=dct(k2,l2), Yq(k3,l3)=dct(k3,l3) if m=1 then zmodyfikuj Yq(k1,l1),Yq(k2,l2),Yq(k2,l2) aby spełniały zależności: Yq(k1,l1)>Yq(k3,l3)+d Yq(k2,l2)>Yq(k3,l3)+d else zmodyfikuj Yq(k1,l1),Yq(k2,l2),Yq(k2,l2) aby spełniały zależności: Yq(k1,l1)+d<Yq(k3,l3) Yq(k2,l2)+d<Yq(k3,l3) end if wstaw zmodyfikowane współczynniki do bloku
Odczytywanie znaku
wybierz pozycję współczynników (k1,l1),(k2,l2),(k3,l3) Yq(k1,l1)=dct(k1,l1), Yq(k2,l2)=dct(k2,l2), Yq(k3,l3)=dct(k3,l3) If Yq(k1,l1)>Yq(k3,l3)+d and Yq(k2,l2)>Yq(k3,l3)+d then m=1 else if Yq(k1,l1)+d<Yq(k3,l3) and Yq(k2,l2)+d<Yq(k3,l3) then m=0 end if
Do pracy!
Koniec tej teorii 🙂 czas zabierać się za implementację! Pisania kodu trochę będzie, ale to dobrze bo od ponad tygodnia nic w StegoCore nie dodawałem. Poznałem na czym opiera się kompresja JPEG i jak można ją wykorzystać do ukrycia danych. Algorytm Zhao & Koch nie wydaje się trudny i z samego pseudokodu można odnieść wrażenie że powinien działać. Wszystko jednak wyjdzie w testach, ale jestem dobrej myśli 🙂


