Kolejnym krokiem rozwoju biblioteki StegoCore jest implementacja algorytmu ukrywania danych, który będzie odporny na kompresję JPEG. Aby lepiej zrozumieć zasadę jego działania, należy zacząć od przedstawienia samego formatu JPEG. Jak wygląda kodowanie i dekodowanie pliku graficznego w kompresji JPEG? W jaki sposób zmienić plik jpeg, aby umieścić w nim sekretne dane? Odpowiedzi na te inne pytania w poniższym poście.

Co to jest JPEG i po co został wymyślony?

W celu ujednolicenia algorytmów kompresji obrazów monochromatycznych i kolorowych, powstał format JPEG. Jest on jednym z najczęściej stosowanych formatów grafiki rastrowej. Algorytm kompresji używany w formacie JPEG jest algorytmem stratnym. Oznacza to, że po skompresowaniu obrazu kosztem utraty niektórych informacji zmniejszamy jego rozmiar. Niemniej jednak, w zależności od wyboru stopnia kompresji, jest możliwość uzyskania jak najmniejszego pliku przy zadowalającej jakości.

Wymienione właściwości sprawiają, że format kompresji JPEG będzie dobrym w kontekście stosowania go jako nośnik steganograficzny. Sama kompresja niesie ze sobą sporo problemów, jednak popularność tego formatu zmniejsza ryzyko ewentualnego ataku. Jedną z pożądanych cech zaproponowanego algorytmu będzie odporność na kompresję JPEG. Oznacza to, że pomimo skompresowania obrazu nadal będzie możliwość odczytania ukrytej wiadomości. Aby dowiedzieć się od czego zależy to, czy daną wiadomość będzie można odczytać po kompresji, należy przyjrzeć się algorytmowi JPEG.

Algorytm kompresji

Algorytm kompresji JPEG jest algorytmem symetrycznym. Oznacza to, że operacje wykonywane podczas dekompresji, wykonują się w odwrotnej kolejności w stosunku do kompresji. W celu uproszczenia operacji zakłada się, że szerokość i wysokość obrazu są wielokrotnością 8. Jeśli warunek ten, nie jest spełniony, należy tego dokonać przed dodanie odpowiedniej ilości wierszy i kolumn.

Podczas kompresji obrazu możemy wyróżnić 6 następujących kroków.

Krok 1.

Pierwszym krokiem jest przejście do modelu luminancja-chrominancja. Zakładamy, iż wejściowy obraz zapisany w postaci modelu (R – ang. red – czerwony, G – ang. green – zielony, B – ang. blue – niebieski), a każda składowa jest liczbą całkowitą zawierającą się w przedziale . Przejście do modelu luminancja-chrominancja odbywa się w następujący sposób:

Krok ten jest pomijany, jeśli wejściowym obrazem jest obraz monochromatyczny.

Krok 2.

Po wykonaniu pierwszego kroku, otrzymujemy obraz zapisany w modelu luminancja-chrominancja. Następnie obraz jest dzielony na bloki 8×8 o rozmiarze pikseli. Dla każdej składowej YCbCr modelu tworzona jest macierz o podanych rozmiarach, aby działania na nich mogły być przeprowadzane niezależnie od siebie.

W celu uproszczenia obliczeń dokonywanych w następnych krokach, od każdego elementu macierzy odejmowana jest wartości równa połowie zakresu, czyli 128. W wyniku tego działania wszystkie elementy macierzy będą z zakresu [-128;127]. Przyjmijmy, iż po wykonaniu tego kroku każdy blok (macierz) można zapisać w następującej postaci:

Krok 3.

Dla każdego bloku obliczana jest dyskretna dwuwymiarowa transformata kosinusowa, zadana wzorem:

W wyniku otrzymamy macierz zawierającą wartości rzeczywiste. Zamiast samych wartości pikseli, mamy ich wartości średnie oraz częstotliwość zmian wewnątrz całego bloku. W przypadku dokładnych obliczeń nie tracimy żadnych danych, gdyż dyskretna transformata kosinusowa jest odwracalna.

Krok 4.

W wyniku obliczeń poprzednich kroków otrzymaliśmy macierz F, która jest transformatą kosinusową bloku danych f. W tym kroku wykonywana będzie operacja zwana kwantyzacją. Polega ona na usunięciu danych, które są mało lub wcale nie widoczne dla ludzkiego oka. Z postaci transformaty wynika, iż znajdują się one w prawej dolnej części macierzy. Proces kwantyzacji można podzielić na dwie części. W pierwszej, każdy element macierzy dzielony jest przez odpowiadającą mu stałą. Następnie otrzymane wartości zaokrąglane są do najbliższej liczby całkowitej. W wyniku tego zaokrąglenia, tracimy pewne dane. Jednak, jak zostało wspomniane, są to dane mało widoczne dla ludzkiego oka.

Stałe wykorzystywane w procesie kwantyzacji ułożone są w macierz zwaną macierzą kwantyzacji. Wartości tych stałych stanowią o tym w jakim stopniu wykonana zostanie kompresja obrazu – im większe one będą, tym więcej informacji zostanie utraconych. Po zaokrągleniu wiele elementów macierzy będzie równe zeru, co wpływa na rozmiar skompresowanego obrazu. Po procesie kodowania będą zajmować mniej miejsca.

Kwantyzację można przedstawić według następującej zależności

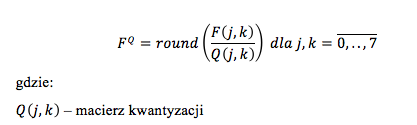
Macierz kwantyzacji decyduje o stopniu kompresji obrazu. Im wyższe są wartości jej elementów, tym wyższa kompresja. Jako przykład można podać macierz znajdującą się w dokumencie standaryzującym kompresję JPEG:

Współczynniki w macierzy zostały tak dobrane, aby uzyskana w wyniku kwantyzacji tablica zawierała jak największą liczbę zer. Zerowy element w jakimkolwiek miejscu w macierzy oznacza utratę pewnych informacji obrazu. Ważne jest, aby były one jak najmniej znaczące i mało widoczne dla oka ludzkiego. Takie informacje znajdują się w prawej, dolnej części macierzy . Natomiast w macierzy współczynniki znajdujące się w prawej, dolnej części są większe od pozostałych. W wyniku kwantyzacji otrzymamy dużą liczbę zer właśnie w tym obszarze macierzy.

Krok 5 i 6

Krok 5 to  przygotowanie danych do kodowania. W tym celu macierz transformowana jest na wektor według algorytmu zig-zag. Kolejność elementów w wektorze można przedstawić następująco:

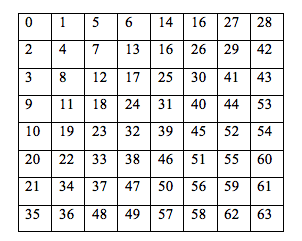
Dzięki temu otrzymany ciąg będzie zawierał dużą liczbę zer, które dodatkowo będą znajdować się obok siebie. Pozwoli to na zastosowanie kodowania, które zmniejszy liczbę bitów potrzebną do zapisania skompresowanego obrazu.

Ostatnim krokiem jest kodowanie entropijne. Idea tego kodowania polega na zastąpieniu najczęściej występujących elementów krótszymi słowami kodowymi. Jest to zwykłe kodowanie Huffmana, dlatego nie będę go prezentował.

Podsumowując algorytm kodera można przedstawić jak poniżej:

Algorytm Dekompresji

Algorytm dekompresji JPEG jest odwróceniem algorytmu kompresji. Oznacza to, że operacje przeprowadzane są w odwrotnej kolejności. Wejściowy, skompresowany obraz dzielony jest na bloki, po czym każdy z nich przekształcany jest w dekoderze bitowym wykorzystującym tablice kodowe Huffmana. Po zastosowaniu algorytmu odwrotnego zig-zag, wektor zamieniany jest w tablice . Otrzymana tablica mnożona jest przez macierze kwantyzacji, w wyniku czego otrzymujemy przybliżoną tablice współczynników transformaty kosinusowej. Ostatnim krokiem jest obliczenie odwrotnej transformaty. Schemat algorytmu dekompresji można przedstawić następująco:

Pliki graficznego w formacie JPEG to dobry nośnik steganograficzny?

Tak jak wspomniałem na początku, pliki zapisane w formacie JPEG ze względu na swoje właściwości mogą być dobrymi nośnikami steganograficznymi. Aby wiadomość ukryta w obrazie była odporna na kompresję, musi zostać wstawiona w dziedzinie transformaty. Wadą tego rozwiązania będzie ilość bitów, którą można zakodować, gdyż zbyt duże modyfikacje spowodują widoczne zmiany w obrazie. Oczywiście zależy to również od obrazu, ponieważ nie we wszystkich miejscach w obrazie jest możliwość zapisania wiadomości. Nie zmienia to jednak faktu, iż ukrycie wiadomości w taki sposób, aby kompresja JPEG nie w usunęła jej z obrazu jest jednym z priorytetów algorytmu.

W którym miejscu można ukryć dane?

Z przeprowadzonych testów wiemy, że na pewno nie w najmniej znaczących bitach pikseli obrazu. Wtedy bowiem, podczas kompresji JPEG dane te są tracone (krok 4, czyli kwantyzacja). Możemy więcej spróbować tak zmodyfikować macierz 8×8 pikseli i w nich ukryć bity sekretu. Opis jak tego dokonać w kolejnym poście, w którym przedstawię pełny algorytm ukrywania danych.